You have now found out quite a lot about the customer's problem, and fluid flow in general. However, you still don't have a design to provide a range of flow-rates to your customer. You have observed that the pressure drop is proportional to flow-rate in the laminar regime, and proportional to the square of the flow-rate for turbulent flow. However, the flow-rates specified by the customer span the laminar, transitional, and turbulent regions. The transitional region is especially problematic because if you specify a certain pressure drop you are not sure what the flow-rate will be from one moment to the next!
Perhaps looking at the Reynolds number for this system will give you a way to design a reliable pumping system for the customer. Remember that the Reynolds number can be used to characterize flow in many different situations.
The Reynolds Number:
![]()
- D is the diameter of the pipe
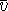 is the average
velocity of the fluid,
is the average
velocity of the fluid, 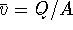 , where A is the cross sectional area of the pipe
, where A is the cross sectional area of the pipe
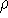 is the density of the fluid
is the density of the fluid
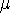 is the
viscosity of the fluid
is the
viscosity of the fluid
- Re is a dimensionless number.
![]()
Previous Page . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Next Page